Phew, this one took a while to get right. My naive attempts was way to slow so I reached for Dijkstras shortest path algorithm… and that payed off pretty well for part 2 ![]()
~1s on my machine, I have not bothered to cleanup and optimize it yet… you have been warned ![]()
I initially went with :digraph, since that is already part of the BEAM:
I felt that that was cheating since that did 90% of the given problem. Therefore, I also implemented Dijkstra naively based on the Wikipedia description of the algorithm.
:digraph was the thing I was looking for, I knew there were something like that already bundled but didn’t remember the name ![]()
Is there a way to get “all the distances” (djikstra table) from :digraph? It was quick enough to :digraph.get_short_path(g, <a>, goal) for every a though…
I don’t think that there’s a way to calculate multiple paths at once with digraph. The performance was good enough though that I didn’t even check.
I went with a naive depth first search. Simply filtering the redundant paths proved to be fast enough (not very fast, exercise took 30s on my machine).
defmodule HillClimbing do
@moduledoc """
Reach the top.
"""
defmodule PartOne do
@moduledoc "First puzzle."
@doc "Solve the first puzzle."
@spec run(String.t()) :: integer()
def run(input) do
input
|> HillClimbing.parse()
|> find_route_to_top()
end
defp find_route_to_top({heights, start, finish}) do
MapSet.new([[start]])
|> HillClimbing.route_length_to_top(heights, finish)
end
end
defmodule PartTwo do
@moduledoc "Second puzzle."
@doc "Solve the second puzzle."
@spec run(String.t()) :: integer()
def run(input) do
{heights, _start, finish} = HillClimbing.parse(input)
heights
|> Enum.filter(&Kernel.==(elem(&1, 1), 0))
|> Enum.reduce(MapSet.new(), fn {start, _height}, routes -> MapSet.put(routes, [start]) end)
|> HillClimbing.route_length_to_top(heights, finish)
end
end
@type location :: {integer, integer}
@type heights :: %{required(location()) => integer()}
@doc "Parse the height_map."
@spec parse(String.t()) :: {heights(), location(), location()}
def parse(input) do
{heights, start, finish, _y} =
input
|> String.split("\n")
|> Enum.reduce({%{}, nil, nil, 0}, fn line, {heights, start, finish, y} ->
parse_line(line, heights, start, finish, y)
end)
{heights, start, finish}
end
defp parse_line(line, heights, start, finish, y) do
{heights, start, finish, y, _x} =
line
|> String.graphemes()
|> Enum.reduce({heights, start, finish, y, 0}, fn height, {heights, start, finish, y, x} ->
case height(height) do
:start -> {Map.put(heights, {y, x}, height("a")), {y, x}, finish, y, x + 1}
:finish -> {Map.put(heights, {y, x}, height("z")), start, {y, x}, y, x + 1}
height -> {Map.put(heights, {y, x}, height), start, finish, y, x + 1}
end
end)
{heights, start, finish, y + 1}
end
defp height(<<h::utf8>>) when h in ?a..?z, do: h - ?a
defp height("S"), do: :start
defp height("E"), do: :finish
@spec route_length_to_top(MapSet.t([location()]), heights(), location()) :: non_neg_integer()
def route_length_to_top(routes, heights, finish) do
routes
|> filter()
|> Enum.reduce_while(MapSet.new(), fn route, candidates ->
{:cont, candidates}
|> add_candidate(route, heights, finish, :left)
|> add_candidate(route, heights, finish, :right)
|> add_candidate(route, heights, finish, :up)
|> add_candidate(route, heights, finish, :down)
end)
|> case do
{:finish, length} -> length
routes -> route_length_to_top(routes, heights, finish)
end
end
defp filter(routes) do
routes
|> Enum.uniq_by(&List.first/1)
end
defp add_candidate({:halt, acc}, _route, _heights, _finish, _direction), do: {:halt, acc}
defp add_candidate(
{:cont, candidates},
[current_location | previous_locations] = route,
heights,
finish,
direction
) do
next_location = next_location(current_location, direction)
if valid?(
Map.get(heights, next_location),
Map.get(heights, current_location),
next_location,
previous_locations
) do
if next_location == finish do
{:halt, {:finish, length(route)}}
else
{:cont, MapSet.put(candidates, [next_location | route])}
end
else
{:cont, candidates}
end
end
defp next_location({y, x}, :left), do: {y, x - 1}
defp next_location({y, x}, :right), do: {y, x + 1}
defp next_location({y, x}, :up), do: {y - 1, x}
defp next_location({y, x}, :down), do: {y + 1, x}
defp valid?(nil, _current_height, _next_location, _previous_locations), do: false
defp valid?(next_height, height, _n, _ps) when next_height > height + 1, do: false
defp valid?(_next_height, _current_height, next, prevs), do: not Enum.member?(prevs, next)
end
Hey, I did not yet know the Enum.with_index/1 function… That wil make the parsing much less cumbersome ![]() Thanks!
Thanks!
After spending the last few days with Erlang. I am back to my comfort zone with this one.
So I used :digraph. And for part 2, I did the naive approach of shortest pathing all the a-s, while caching an encountered a. Solves in 2 seconds, but I think I can improve by starting from destination and spreading outwards. (maybe BFS from the destination and stopping at first a or something?) I’ll come back to this on weekend. For now, this is how my solution looks like:
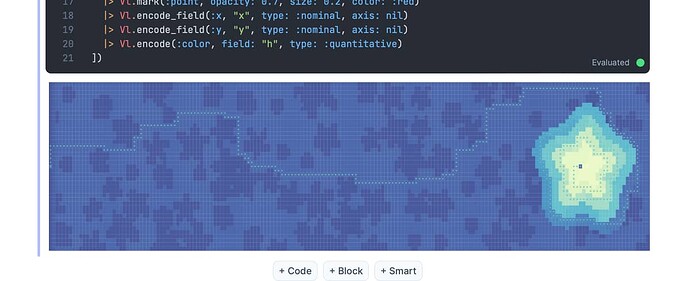
Took it as an opportunity to learn me some Vegalite too.
Thank you @kwando for inspiring me to do so.
Basic stuff, will dive deeper at night.
Update: I could add animation to the first part. The second part graph looks ugly though. I need to play more with this stuff. This is amazing stuff!
Here’s the code for Livemd version: https://github.com/code-shoily/advent_of_code/blob/master/lib/2022/day_12.livemd
And the regular one (This one has cache based part 2 since I don’t need to worry about any graphs) advent_of_code/lib/2022/day_12.ex at master · code-shoily/advent_of_code · GitHub
Like most I used :digraph. Felt like cheating actually. Though after Day 11 I wasn’t above taking the easy path.
Pun intended.
AOCDay12
defmodule Day12 do
defmodule Input do
def sample_data() do
"""
Sabqponm
abcryxxl
accszExk
acctuvwj
abdefghi
"""
end
@neighbors [{-1, 0}, {1, 0}, {0, -1}, {0, 1}]
def parse(input) do
rows =
input
|> String.split("\n", trim: true)
{row_len, col_len} = {length(rows), String.length(hd(rows))}
rows
|> populate_vertices()
|> populate_edges(row_len - 1, col_len - 1)
end
defp populate_vertices(input_rows) do
input_rows
|> Enum.with_index()
|> Enum.reduce({:digraph.new(), nil, nil}, fn {line, r}, {graph, start, stop} ->
String.codepoints(line)
|> Enum.with_index()
|> Enum.reduce({graph, start, stop}, fn {<<val::utf8>>, c}, {g, begin, final} ->
case val do
83 ->
:digraph.add_vertex(g, {c, r}, ?a)
{g, {c, r}, final}
69 ->
:digraph.add_vertex(g, {c, r}, ?z)
{g, begin, {c, r}}
_ ->
:digraph.add_vertex(g, {c, r}, val)
{g, begin, final}
end
end)
end)
end
defp populate_edges({graph, start, stop}, rows, cols) do
edged_graph =
for r <- 0..rows,
c <- 0..cols,
reduce: graph do
graff ->
{emanating_vertex, v1} = :digraph.vertex(graff, {c, r})
@neighbors
|> Enum.reduce(graff, fn {x, y}, gr ->
incident = :digraph.vertex(graff, {c + x, r + y})
case incident do
{incident_vertex, v2} when v2 - v1 == 1 ->
:digraph.add_edge(gr, emanating_vertex, incident_vertex)
gr
{incident_vertex, v2} when v2 - v1 <= 0 ->
:digraph.add_edge(gr, emanating_vertex, incident_vertex)
gr
_ ->
gr
end
end)
end
{edged_graph, start, stop}
end
end
def part1({graph, start, stop}) do
:digraph.get_short_path(graph, start, stop) |> Enum.count() |> Kernel.-(1)
end
def part2({graph, _start, stop}) do
graph
|> :digraph.vertices()
|> Enum.filter(fn vertex -> {vertex, ?a} == :digraph.vertex(graph, vertex) end)
|> Enum.map(fn starter -> :digraph.get_short_path(graph, starter, stop) end)
|> Enum.filter(& &1)
|> Enum.map(fn path -> Enum.count(path) - 1 end)
|> Enum.min()
end
Like others, used :digraph. Figured the built-in BFS would be fine for the unweighted graph.
Brute forced part 2 since exec time was reasonable. Could probably improve by doing a signle BFS with a modified termination condition (i.e. ends at some a and no path < the respective a’s distance). Might revisit if I find some time.
I don’t know if the algorithm I’ve used has a name, but part 2 took ~20 ms on my machine ![]()
defp walk([{position, distance} | rest], map) do
if map[position].distance == :unknown do
new_map = put_in(map, [position, :distance], distance)
possible_ways = where_can_i_go(position, map) |> Enum.map(fn p -> {p, distance + 1} end)
walk(rest ++ possible_ways, new_map)
else
walk(rest, map)
end
end
Looks like some variant of Djikstra ![]() nice implementation
nice implementation ![]()
As someone without a CS background I knew I would have some homework to do before tacking this one so here I am a week later ![]()
I settled on a variation of Djikstra with a heuristic (A*?) which worked great for part 1 once I worked out a few hard to find bugs. I tried to be clever on part 2 by reversing the search while rechecking the heuristic for the closest “a” node after each step, but it was off by a few steps, I am guessing because I didn’t test whether it was actually reversible. I was too lazy to figure out a way to do that so I just brute forced it which worked fine (< 30 secs).