Advent of Code 2022 - Day 14

[Aetherus]

Stream.unfold helps a lot.

Aetherus/advent-of-code/blob/master/2022/day14.livemd

[hauleth]

advent-of-code/day14.livemd at master · hauleth/advent-of-code · GitHub - my solution

[kwando]

My solution, my naive approach worked fine. Was worried I needed to come up something smarter for part 2, but it was quick enough.

kwando/AoC2022/blob/main/14/day14.livemd

[code-shoily]

This is how my part 1 and 2 look like: (My browser crashed while attempting to animate part 2 though)

Part 1

Part 2

livemd - https://github.com/code-shoily/advent_of_code/blob/master/lib/2022/day_14.livemd

[hauleth]

Ok, so I will also add visualisations (as LiveMD do not store them )

Part 1

Part 2

[stevensonmt]

Y’all getting soo fancy with it!

I way overcomplicated this one in my mind. I thought initially it was going to be another pathfinding problem and set up my data structure as another digraph. After realizing it wasn’t that, I left it b/c part 1 worked with a naive approach anyway.
On part 2 I spent a ton of time trying think of a way to do something clever with just adding edges, and using the lengths of the edges to do the calculations without actually tracking the sand. I thought I just need the area of the triangle that will be formed minus the number of rocks and the number of protected spaces. I still think that should work but I couldn’t figure out how to properly calculate the protected spaces for the more complex arrangement of the real data. The simple sample data worked great. Anyway, I ended up just using the same approach for both with a minor tweak for part 2 and it was still fast enough.

  defmodule Solve do
    @sand_falls [{0, 1}, {-1, 1}, {1, 1}]

    @origin {500, 0}

    def sand_falling({x, y}, graph, limit, floor?) do
      if off_grid?(y, limit) and not floor? do
        {:off_grid, graph}
      else
        dir_falling =
          @sand_falls
          |> Enum.find(fn {dx, dy} -> can_fall?({dx + x, dy + y}, graph) end)

        case dir_falling do
          nil ->
            :digraph.add_vertex(graph, {x, y}, :sand)

            if floor? and {x, y} == @origin do
              {:stuck_at_origin, graph}
            else
              {:at_rest, graph}
            end

          {dx, dy} ->
            sand_falling({dx + x, dy + y}, graph, limit, floor?)
        end
      end
    end

    def off_grid?(y, max_y) do
      y > max_y
    end

    defp can_fall?({x, y}, graph) do
      case :digraph.vertex(graph, {x, y}) do
        false -> true
        _ -> false
      end
    end

    def solve(graph, limit, floor?) do
      [1]
      |> Stream.cycle()
      |> Enum.reduce_while({graph, 0}, fn i, {g, count} ->
        case sand_falling(@origin, g, limit, floor?) do
          {:at_rest, g} -> {:cont, {g, count + i}}
          # only reachable with floor? == false
          {:off_grid, _g} -> {:halt, count}
          # only reachable with floor? == true, includes the sand that didn't drop b/c stuck at origin
          {:stuck_at_origin, _g} -> {:halt, count + i}
        end
      end)
    end

    def part1({graph, limit}) do
      solve(graph, limit, false)
    end

    def part2({graph, limit}) do
      floor = limit + 2

      graph =
        for x <- (500 - floor)..(500 + floor), reduce: graph do
          g ->
            :digraph.add_vertex(g, {x, floor}, :floor)
            g
        end

      solve(graph, floor, true)
    end
  end

Full parsing and bonus render function for drawing on the terminal on github.

[Aetherus]

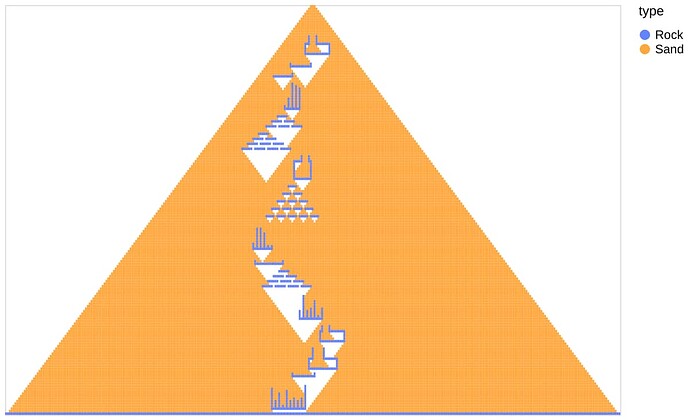
Seems this thread has become a gallery

I feel I have to post my pictures, too. I’m definitely not a VegaLite guru, though.

Part 1

Part 2

[stevensonmt]

Reading over some of the solutions here and I’m curious about using Stream.unfold/2. Is there some benefit to this followed by a count versus an Enum.reduce with a counter? Or could you eliminate the need for a separate count step by including a count in the unfolding accumulator?

[Aetherus]

Stream.unfold/2 returns a stream, and all streams are lazy, meaning if you don’t want a value, it does nothing.

I use Stream.unfold/2 because, in the beginning, I don’t have an enumerable (certainly I’m not going to iterate over my input), and I’m too lazy to write my own recursive function that generates the next state based on the previous state

I can introduce a counter in the unfolding step, but even so, I still need to iterate over the stream to find the correct state and its counter value. In the end, it’s of the same performance as |> Enum.count().

[stevensonmt]

Ah, thanks for the explanation. Now that you explained that my solution of creating an enumerable that I could reduce with Stream.cycle([1]) seems like an ugly way to accomplish the same thing. Always learning, which is why I love AoC.

[tfwright]

Another easy one to help me catch up. No issues here aside from an off-by-1 error on my first attempt to calculate part 2

https://gist.github.com/tfwright/dc9cb2aff138c34d65bbba8bbb0420a6

[al2o3cr]

I used an :ets property that I’d never needed to before - with an :ordered_set table :ets.next will take a key that doesn’t exist in the table and find the “next” one in term order that does.

For instance, if the table has keys that are {x, y}, then :ets.next(t, {500, 0}) will handle the “drop to the first occupied spot” efficiently.

https://gist.github.com/al2o3cr/a5d0473675d666d1a6d1c5e947787742

[hauleth]

TIL, nice