I couldn’t find a faster solution in part 2, so I just brute-forced my way. I’m looking forward to smarter solutions.
I did the same for part 2, took 12 seconds. On reddit someone suggested quad trees, I tried it and I’m down to less than 1.5 second.
On slack someone suggested an even better way (~4 ms) but I’m too lazy to try it ![]()
I didn’t find a smarter way for part 2 either, brute forcing it worked but took a while. I had some idea about calculating how much sensors overlap on a given row and then use that number to skip checking rows, but I didn’t get it to work ![]()
I came up with an idea that involves a little bit of linear algebra:
- Rotate the whole map by 45 degrees to the left, so that the diamond-shaped sensor coverages become square.
- If there is a point covered by no sensor, there must be a sqrt(2)-unit-wide gap between some pair of the vertical edges of those squares, and a sqrt(2)-unit-high gap between some pair of the horizontal edges of those squares. (by the way, I can do this because there’s no 2x2 sensor)
- Find that point and convert it back to its original position.
The problem is, there are multiple such gaps ![]()
The good news is, there are not so many such gaps. I can just try all the results util I pass the quiz ![]()
Here’s my new code:
# matrix for turning left 45 degrees
# and stretch by the factor sqrt(2).
# It's not a unit matrix because I don't want to deal with irrational numbers.
@m {
{1, -1},
{1, 1}
}
# inverse of @m
@inv_m {
{0.5, 0.5},
{-0.5, 0.5}
}
# `sensors` is a list of {xc, yc, r}
# where `xc` and `yc` is the coordinate of the center of a sensor,
# and `r` is its manhattan radius.
def part2_v2(sensors) do
sensors =
sensors
|> Enum.map(fn {xc, yc, r} ->
{
mul(@m, {xc - r, yc}), # left corner --> bottom-left corner
mul(@m, {xc + r, yc}) # right corner --> top-right corner
}
end)
x_pairs =
sensors
|> Enum.flat_map(fn {{x1, _}, {x2, _}} ->
[x1, x2]
end)
|> Enum.uniq()
|> Enum.sort()
|> Enum.chunk_every(2, 1, :discard)
# because the map is stretched by factor sqrt(2),
# the sqrt(2)-unit-wide gaps become 2-unit wide.
|> Enum.filter(fn [x1, x2] -> x2 - x1 == 2 end)
y_pairs =
sensors
|> Enum.flat_map(fn {{_, y1}, {_, y2}} ->
[y1, y2]
end)
|> Enum.uniq()
|> Enum.sort()
|> Enum.chunk_every(2, 1, :discard)
|> Enum.filter(fn [y1, y2] -> y2 - y1 == 2 end)
for [x1, x2] <- x_pairs, [y1, y2] <- y_pairs do
x = (x1 + x2) / 2
y = (y1 + y2) / 2
{x, y} = mul(@inv_m, {x, y})
IO.inspect(x * 4_000_000 + y)
end
end
defp mul(
{
{a, b},
{c, d}
},
{x, y}
) do
{
a * x + b * y,
c * x + d * y
}
end
Quad tree is interesting, though I’m not sure how to solve this quiz with it.
I solved part 1 by brute force.
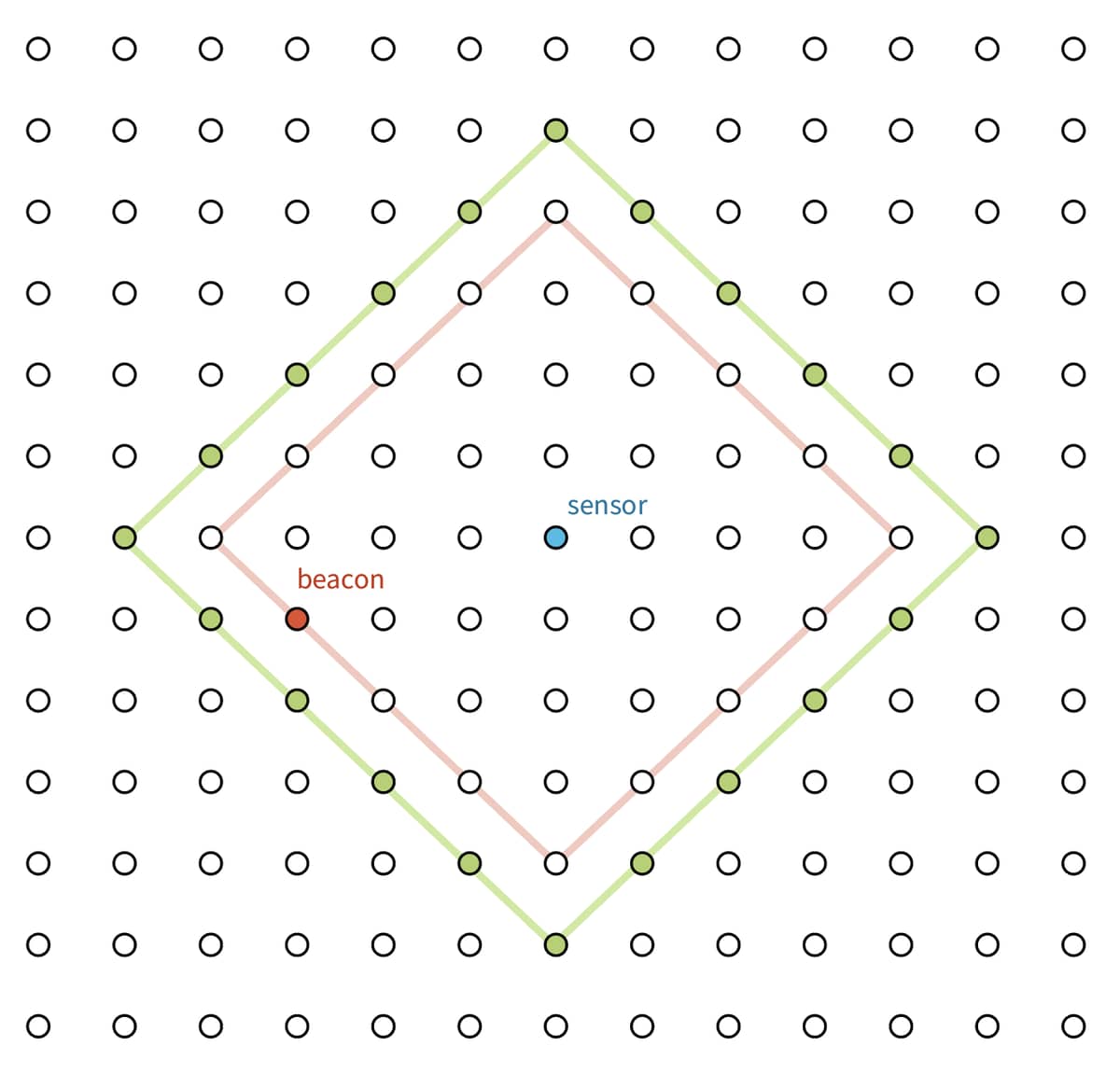
For part 2, after brute-force not working on 4,000,000 x 4,000,000 (I wonder why?), I thought about “walking the edges”:
The idea is that for each pair of Sensor–Beacon, we can be sure the outlying (solution) beacon cannot be under the red line. Given that within x = 0…4M, y = 0…4M there is only one possible solution, the solution beacon would have to fall under the green line.
More specifically, it should be the point which falls under the most green lines:
So my Part 2 solution is iterating over each sensor–beacon pair to trace the points under the green line (Manhattan distance + 1), and find the most overlap. The code can be further optimized, but I was just happy it worked…
def part_2(input \\ "test") do
coord =
input
|> load_data()
|> Enum.map(&parse_structured_data/1)
edges =
for [{s_x, s_y}, {b_x, b_y}] <- coord do
list_outside_edges({s_x, s_y}, {b_x, b_y})
end
edges
|> List.flatten
|> Enum.frequencies
|> Enum.sort_by(fn {_, v} -> v end, :desc)
|> Enum.at(0)
end
def list_outside_edges({x, y}, {b_x, b_y}) do
d = manhattan_distance({x, y}, {b_x, b_y}) + 1
edges_no_top_corners = for i <- 0..d-1 do
[
{x-d+i, y+i},
{x-d+i, y-i},
{x+d-i, y-i},
{x+d-i, y+i}
]
end
[{x, y-d} | [{x, y+d} | edges_no_top_corners]]
|> List.flatten
|> Enum.uniq
end
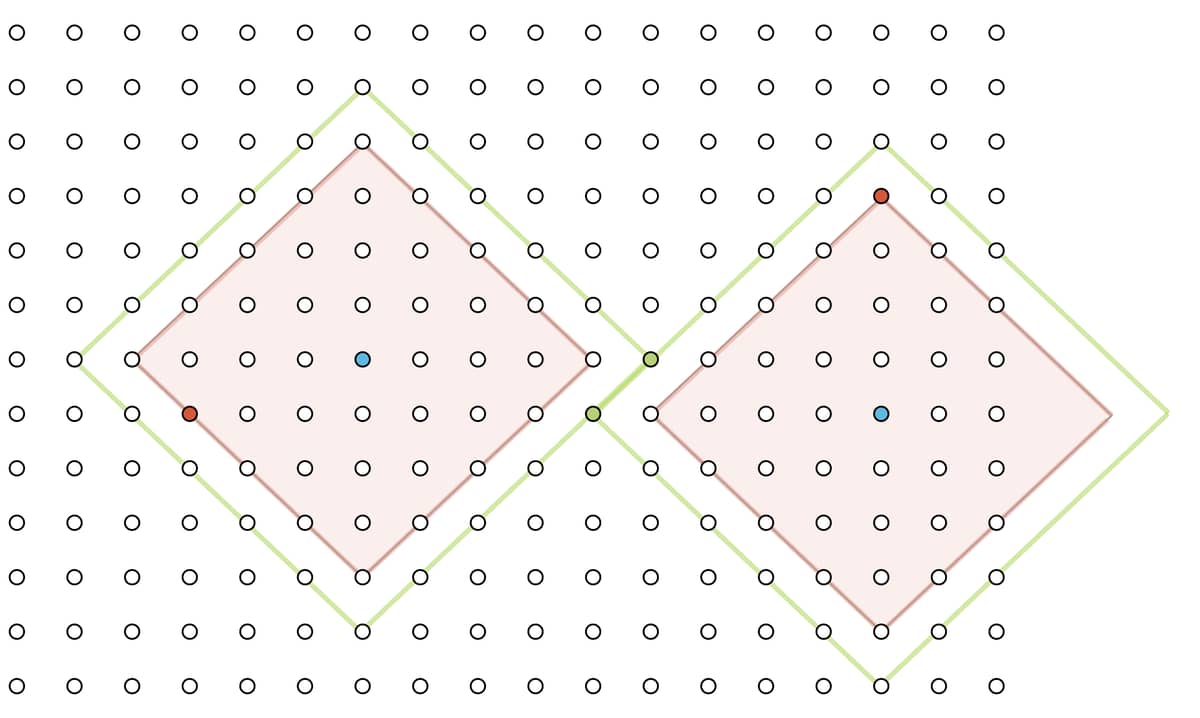
Well to use quad trees at each step I checked if the four corners of a quad (a square) were in range of the same sensor. If yes then the quad is fully covered. Otherwise I would split the quad and check recursively.
At some point you end up with a quad of size 1x1 that is not covered, and that is the solution.
It is not very efficient, but at the time the solution is found there are only 33 different quads in my tree, with my input.
I figured I only need to do some simple filtering then I can get the true result. It takes less than 500 microseconds on my laptop.
# matrix for turning left 45 degrees
# and stretch by the factor sqrt(2)
@m {
{1, -1},
{1, 1}
}
# inverse of @m
@inv_m {
{0.5, 0.5},
{-0.5, 0.5}
}
# `sensors` is a list of {xc, yc, r}
# where `xc` and `yc` is the coordinate of the center of a sensor,
# and `r` is its manhattan radius.
def part2_v2(sensors) do
sensors =
sensors
|> Enum.map(fn {xc, yc, r} ->
{
# left corner --> bottom-left corner
mul(@m, {xc - r, yc}),
# right corner --> top-right corner
mul(@m, {xc + r, yc})
}
end)
x_pairs =
sensors
|> Enum.flat_map(fn {{x1, _}, {x2, _}} ->
[x1, x2]
end)
|> Enum.uniq()
|> Enum.sort()
|> Enum.chunk_every(2, 1, :discard)
|> Enum.filter(fn [x1, x2] -> x2 - x1 == 2 end)
y_pairs =
sensors
|> Enum.flat_map(fn {{_, y1}, {_, y2}} ->
[y1, y2]
end)
|> Enum.uniq()
|> Enum.sort()
|> Enum.chunk_every(2, 1, :discard)
|> Enum.filter(fn [y1, y2] -> y2 - y1 == 2 end)
for [x1, x2] <- x_pairs,
[y1, y2] <- y_pairs,
x = div(x1 + x2, 2),
y = div(y1 + y2, 2),
p = {x, y},
!Enum.any?(sensors, &cover?(&1, p)),
{x, y} = mul(@inv_m, p),
do: x * 4_000_000 + y
end
defp cover?({{x1, y1}, {x2, y2}}, {x, y}) do
x in x1..x2 and y in y1..y2
end
defp mul(
{
{a, b},
{c, d}
},
{x, y}
) do
{
trunc(a * x + b * y),
trunc(c * x + d * y)
}
end
Part 2 just about broke me. Finally got what is basically a brute force method that works fast enough for me. 12-14 seconds to get the answer. I was really struggling, trying to use MapSet operations to track each row rather than a Range. Seeing @Aetherus use of Range.disjoint/2 was a huge help.
def part2({sensors, _beacons_by_row}, limit) do
{y, rng} =
0..limit
|> Stream.map(&{&1, sensors |> filter_for_row(&1) |> sensed_at_y(&1) |> unsensed(limit)})
|> Enum.find(fn {_y, rngs} ->
match?([{_a, _b}], rngs)
end)
[{y, rng}]
|> Enum.map(fn {y, [{s, e}]} -> [{y, div(e + s, 2)}] end)
|> Enum.map(fn [{y, x}] -> x * 4_000_000 + y end)
|> hd()
end
defp filter_for_row(sensors, y) do
sensors |> Enum.reject(fn {{_, s_y}, d} -> abs(y - s_y) > d end)
end
defp sensed_at_y(sensors, target_row) do
sensors
|> Enum.map(fn {{x, y}, taxi_dist} ->
delta = taxi_dist - abs(target_row - y)
{x - delta, x + delta}
end)
end
defp unsensed(sensed_stream, limit) do
sensed_stream
|> Enum.sort()
|> Enum.reduce_while([{0, limit}], fn {s, e}, unsensed ->
case exclude_sensed({s, e}, unsensed) do
[{a, b}] when b - a == 2 ->
{:halt, div(b + a, 2)}
acc ->
{:cont, acc}
end
end)
end
defp exclude_sensed({_s, _e}, []), do: []
defp exclude_sensed({s, e}, [{ss, ee} | ranges]) do
if Range.disjoint?(s..e, ss..ee) do
[{ss, ee} | ranges]
else
cond do
s > ss and e < ee -> [{ss, s - 1} | exclude_sensed({e + 1, ee}, ranges)]
s > ss -> [{ss, s - 1}]
e < ee -> [{e + 1, ee}]
true -> []
end
end
end
Actually, using Range.disjoint?/2 was a mistake. Consider this situation, at some y, there are 3 ranges before merging: 0..10, 11..20, 21..30, how many ranges should there be after merging? There should be only one range, 0..30. But Range.disjoint?/2 will tell you all those ranges are disjoint to each other, so they won’t merge.
I think it works for this exercise b/c there is no difference between [{0..30}] and [{0..10}, {11..20}, {21..30}]. Both indicate a situation where there is more than one item remaining. Also contrary to your method of merging ranges, I was sort of breaking the full range 0…limit up into smaller ranges.
For me this puzzle had the greatest divergence between complexity and difficulty. It was fairly easy to reason about what to do but of course the first naive solution that solved for the test input by tracking the content of every node was far too slow for the actual input.
I solved part 1 after realizing I only needed to track the ranges of intersection on a single line, and then I used that same trick in part 2 to avoid having to check every single point since I could get the intersection for the current x value and then skip to the end of the y range. Took less than 3 secs on my laptop.
Part 1 was a straightforward “generate sets representing coverage at the target coordinate and union them all together” task, but that would have created massive sets for part 2.
Part 2 was saved by the 0..4_000_000 bound - instead of creating a list of all the positions that are covered, the solution subtracts a range for each sensor from the whole range. This removes the need to create a list/set/etc with 4m elements in favor of a maximum of O(sensors) ranges per Y coordinate.
Each Y coordinate is computed entirely separately, so the problem is exactly the sort of “embarrassingly parallel” situation that Task.async_stream helps with. It could stand some tuning (maybe grouping batches of Y-coordinates together?), as it only manages to saturate 2 CPUs on my laptop.