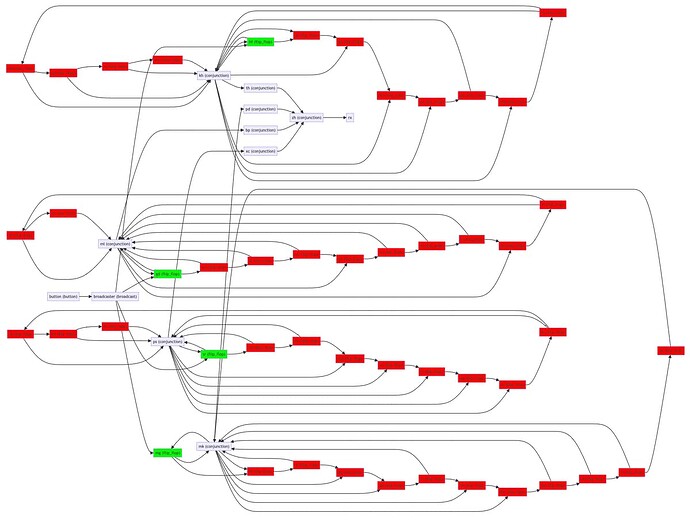
This one lost me at the beginning, but after a little inspection of the input, there is a clear path to the answer.
Explainations in part_two/1
defmodule AdventOfCode.Y23.Day20 do
alias AoC.Input, warn: false
def read_file(file, _part) do
Input.stream!(file, trim: true)
end
def parse_input(input, _part) do
{modules, out_from} = Enum.map_reduce(input, _out_from = %{}, &parse_line/2)
# now for each inverter we need to initialize state will all its possible inputs
modules =
modules
|> Enum.map(fn
{key, {:conj, :uninitialized, outs}} ->
state = Map.new(Map.fetch!(out_from, key), fn k -> {k, 0} end)
{key, {:conj, state, outs}}
other ->
other
end)
|> Map.new()
{modules, out_from}
end
defp parse_line(line, out_from) do
[name, outs] = String.split(line, " -> ")
{name, kind, state} =
case name do
"broadcaster" -> {"broadcaster", :bcast, nil}
"%" <> name -> {name, :flip, :off}
"&" <> name -> {name, :conj, :uninitialized}
end
outs = String.split(outs, ", ")
out_from = Enum.reduce(outs, out_from, fn out, acc -> Map.update(acc, out, [name], &[name | &1]) end)
module = {name, {kind, state, outs}}
{module, out_from}
end
def part_one({modules, _}) do
{count_low, count_high, _} =
Enum.reduce(1..1000, {0, 0, modules}, fn _, {count_low, count_high, modules} ->
{count_low_add, count_high_add, modules} = push_button(modules)
{count_low + count_low_add, count_high + count_high_add, modules}
end)
count_low * count_high
end
def part_two({modules, out_from}) do
# modules =
# Map.new(modules, fn
# {key, {:flip, _, _}} -> {key, :flip}
# {key, {:conj, _, _}} -> {key, :conj}
# {key, {:bcast, _, _}} -> {key, :bcast}
# end)
# Rule:
#
# &jm -> rx
#
# For rx to receive a low pulse, &jm must remember a high pulse for all its
# inputs
#
# Then we have that:
#
# &sg -> jm
# &lm -> jm
# &dh -> jm
# &db -> jm
#
# So we need all of them to send a high input in the same cycle.
#
# The parents are those. Note that sg, lm, dh and db have each one a single
# input, so they are actually regular not gates, or "%" modules.
#
# &bc -> _, _, _, _, dh, _, _
# &bx -> _, _, db
# &qq -> lm, _, _, _, _, _, _
# &gj -> _, _, sg, _
#
# For sg, lm, dh and db to send a high pulse in the same time, we need bc,
# bx, qq and qj to send a low pulse in the same time.
#
# So we count how much cycles it takes for each one to send a low pulse, and
# the LCM of those cycle numbers is the answer.
#
# Though I have a feeling that the input is very tailored for that solution
# because any input would not guarantee that if bc, bx, qq and qj send a low
# pulse after N first cycles, they would acutally send a low pulse every
# other N cycles.
#
cyclics = Enum.flat_map(["rx"], &Map.fetch!(out_from, &1))
cyclics = Enum.flat_map(cyclics, &Map.fetch!(out_from, &1))
cyclics = Enum.flat_map(cyclics, &Map.fetch!(out_from, &1))
counts = count_cycles_until_low_pulse(modules, cyclics)
counts |> Map.values() |> Enum.reduce(fn a, b -> trunc(lcm(a, b)) end)
end
defp count_cycles_until_low_pulse(modules, watch_list) do
infinite_ints = Stream.iterate(1, &(&1 + 1))
cycle_counts = Map.new(watch_list, &{&1, false})
Enum.reduce(infinite_ints, {modules, cycle_counts}, fn i, {modules, cycle_counts} ->
# We cannot inspect the states after the button is pushed because the
# modules we are looking for are resetting before the modules are
# returned.
#
# So we need to inspect the emitted pulses and return from that.
{modules, cycle_counts} =
push_button(modules, cycle_counts, fn pulses, counts ->
Enum.reduce(pulses, counts, fn
{_, 1, _}, counts ->
counts
{from, 0, _}, counts ->
case Map.get(counts, from) do
false -> Map.put(counts, from, i)
_ -> counts
end
end)
end)
if Enum.all?(cycle_counts, fn {_, count} -> count end) do
throw({:counts, cycle_counts})
end
{modules, cycle_counts}
end)
catch
{:counts, counts} -> counts
end
defp push_button(modules) do
init_pulse = {"button", 0, "broadcaster"}
{_count_low, _count_high, _modules} = reduce([init_pulse], modules, 0, 0)
end
defp reduce([], modules, count_low, count_high) do
{count_low, count_high, modules}
end
defp reduce(pulses, modules, count_low, count_high) do
{count_low, count_high} = count_pulses(pulses, count_low, count_high)
{new_pulses, new_modules} =
Enum.flat_map_reduce(pulses, modules, fn {_, _, to} = p, modules ->
case Map.fetch(modules, to) do
{:ok, module} ->
{next_pulses, new_module} = handle_pulse(p, module)
modules = Map.put(modules, to, new_module)
{next_pulses, modules}
:error ->
{[], modules}
end
end)
reduce(new_pulses, new_modules, count_low, count_high)
end
defp push_button(modules, acc, f) do
init_pulse = {"button", 0, "broadcaster"}
{_modules, _acc} = run([init_pulse], modules, acc, f)
end
defp run([], modules, acc, _f) do
{modules, acc}
end
defp run(pulses, modules, acc, f) do
{new_pulses, new_modules} =
Enum.flat_map_reduce(pulses, modules, fn {_, _, to} = p, modules ->
case Map.fetch(modules, to) do
{:ok, module} ->
{next_pulses, new_module} = handle_pulse(p, module)
modules = Map.put(modules, to, new_module)
{next_pulses, modules}
:error ->
{[], modules}
end
end)
new_acc = f.(new_pulses, acc)
run(new_pulses, new_modules, new_acc, f)
end
defp handle_pulse({_, kind, me}, {:bcast, _, outs} = this) do
# There is a single broadcast module (named broadcaster). When it receives a
# pulse, it sends the same pulse to all of its destination modules.
sends = send_all(outs, me, kind)
{sends, this}
end
defp handle_pulse({_, 0, me}, {:flip, state, outs}) do
# if a flip-flop module receives a low pulse, it flips between on and off.
# If it was off, it turns on and sends a high pulse. If it was on, it turns
# off and sends a low pulse.
{new_state, send_kind} =
case state do
:off -> {:on, 1}
:on -> {:off, 0}
end
sends = send_all(outs, me, send_kind)
this = {:flip, new_state, outs}
{sends, this}
end
defp handle_pulse({_, 1, _}, {:flip, _, _} = this) do
# If a flip-flop module receives a high pulse, it is ignored and nothing
# happens.
{[], this}
end
defp handle_pulse({from, kind, me}, {:conj, state, outs}) do
# Conjunction modules (prefix &) remember the type of the most recent pulse
# received from each of their connected input modules; they initially
# default to remembering a low pulse for each input. When a pulse is
# received, the conjunction module first updates its memory for that input.
# Then, if it remembers high pulses for all inputs, it sends a low pulse;
# otherwise, it sends a high pulse.
state = Map.replace!(state, from, kind)
send_kind = if all_high?(state), do: 0, else: 1
sends = send_all(outs, me, send_kind)
this = {:conj, state, outs}
{sends, this}
end
defp all_high?(map) do
Enum.all?(map, fn
{_, 1} -> true
_ -> false
end)
end
defp send_all(outs, me, kind) do
Enum.map(outs, &{me, kind, &1})
end
defp count_pulses([{_, 0, _} | pulses], count_low, count_high) do
count_pulses(pulses, count_low + 1, count_high)
end
defp count_pulses([{_, 1, _} | pulses], count_low, count_high) do
count_pulses(pulses, count_low, count_high + 1)
end
defp count_pulses([], count_low, count_high) do
{count_low, count_high}
end
defp lcm(0, 0), do: 0
defp lcm(a, b), do: a * b / Integer.gcd(a, b)
end