So… that’s it? Everyone is stuck on part 2? 
I looked at Reddit hints and thought I probably wouldn’t have come up with the solution myself in a reasonable time, which made me decide not to proceed with today’s challenge.
I am finally unstuck. 
I managed to solve the problem without any hints from Reddit. I did use WolframAlpha for helping me find the formulas for the sum of some sequences.
My solution is not a general solution. I’ve hard-coded magic numbers specific for my input. I didn’t bother writing a more general solution that would calculate those magic numbers using the code for part 1.
There are some brief comments in the code that gives some hints of how I solved it. I’ve also kept some of the debug code I used for understanding the input.
1 Like
I did not finish on lunch time, I’m trying again. I have found what should work, but I do not get the right answer.
I have the same approach as you @bjorng, but I missed something.
I wonder If adding the cells like I do (with translation of coordinates and uniqueness of course) should work.
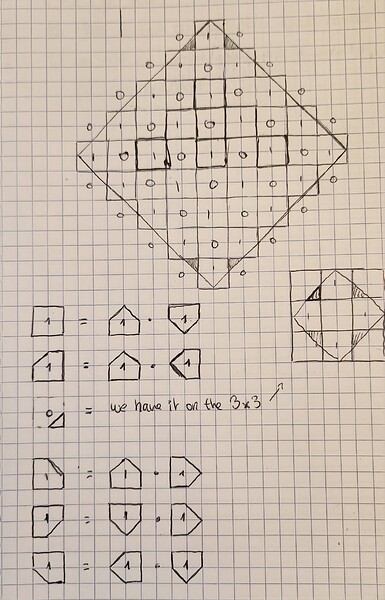
1 means regular fill pattern: the center grid and pointy cells, and corner-cut cells.
0 is the alternate fill, the other full tiles.
Actually @bjorng could you send me your input and solution ? That would help me a lot to find where I am mistaken (given my merging of tiles is correct).
Edit ah come on !
case Map.get(grid, xy) do
"." -> true
_ -> false
end
That stupid bug where I ignore the “S”.
Ok so it works as expected 
Pheew, took so long.
Edit2: Took the time to cleanup. I left a lot of unnecessary checks and redundant assertions that were useful when defining all de different things to compute and how to do it. Full explanation in comments:
It takes 2.8 seconds. 99% of that time is just running the simulation on the 3x3 grid.
1 Like
This one was really painful for me, took me a lot of time to get right. The main bits of realisation that got me through:
- I should imagine the whole thing coloured in a “checkerboard” pattern, and the final picture is going to be the number of either “white” or “black” places (depending on the parity of the input) inside a “ball” of the given radius, centred at “S”. The length is of course counted just going through the allowed places, so that needed to be calculated.
- For part 2, the final mahoosive ball is going to roughly look like a square, centred at ‘S’, rotated 45 degrees (sometimes people call this a ‘diamond’ shape). All the ‘inner’ tiles (ie copies of the original map) are going to be full - so contributing either the number of all ‘white’ or all ‘black’ places in the whole of the original map. For the ‘boundary’ tiles, some calculations need to be made.
- What will make the above thing work is that in the given map, the row and the column going through ‘S’ are free (i.e. no #), and likewise all the rows and columns along the sides. I also checked that there will be no ‘pockets’ left, i.e. the furthest points from the centre ‘S’ are really the corners. (This is why my calculation won’t work for the sample map I think.)
Anyway, even after this, it took me too long to get the calculations right.
Part 1 solution is commented out in the code. It’s not the cleanest… but I am really tired of this question.
code
Mix.install([{:queue, "~> 0.1.0"}, {:ex2ms, "~> 1.0"}])
defmodule Main do
def run() do
get_input()
|> Enum.map(&String.to_charlist/1) |> mkgrid()
|> solve2()
end
# assumptions:
# - square grid, odd dimensions
# - "S" exactly in the middle
# - clear paths horiz and vert through "S" and along all sides
# probably won't work for n close to a multiple of mod (=131)
def get_input() do
# "testinput21.1"
"input21"
|> File.read!() |> String.trim() |> String.split("\n")
end
def mkgrid(ls) do
for {row, r} <- Enum.with_index(ls),
{val, c} <- Enum.with_index(row),
into: %{}, do: {{r,c}, val}
end
def addt({a,b},{c,d}), do: {a+c,b+d}
# uses :q, an empty ets table
# precompute Map.keys(gr)
def dists_from(table,gr,keys) do
qq = Queue.pop(:q)
if qq != nil do
{p,d,tf} = qq
for dir <- [{-1,0},{1,0},{0,1},{0,-1}] do
np = addt(p,dir)
if np in keys and gr[np] != ?# and not :ets.member(table,np) do
Queue.push(:q,{np,d+1,not tf})
:ets.insert(table, {np, d+1, not tf})
end
end
dists_from(table,gr,keys)
end
end
def xor(true,true), do: false
def xor(false,false), do: false
def xor(true,false), do: true
def xor(false,true), do: true
def prep_calc(grid,n) do
par = (rem(n,2) == 1)
{{rc,cc},_} = Enum.find(grid,fn {_,v} -> v == ?S end)
{rmax,_} = Enum.max_by(Map.keys(grid), &elem(&1,0))
{_,cmax} = Enum.max_by(Map.keys(grid), &elem(&1,1))
mod = rmax+1
t1remd = rem(n-1,mod)
t1par = xor( rem(n-t1remd,2)==1 , par)
t2remd = mod+t1remd
t2par = not t1par
ax1remd = rem(n - rc - 1,mod)
ax1par = xor( (rem(n-ax1remd,2) == 1), par)
{ax2remd,ax2par} = {(if ax1remd < rc, do: mod+ax1remd, else: 0), not ax1par}
Queue.new(:q)
for {t,s} <- [{:cc,{rc,cc}}, {:ul,{0,0}}, {:uc,{0,cc}}, {:ur,{0,cmax}}, {:cr,{rc,cmax}},
{:dr,{rmax,cmax}}, {:dc,{rmax,cc}}, {:dl,{rmax,0}}, {:cl,{rc,0}}] do
:ets.new(t, [:named_table])
:ets.insert(t,{s,0,false}) # assuming all starting points are "even"
Queue.push(:q,{s,0,false})
dists_from(t,grid,Map.keys(grid))
end
## part 1 solution:
# :ets.select(:cc,[ {{:"$1", :"$2", :"$3"}, [{:andalso, {:"=<", :"$2", 64}, {:==, :"$3", false}}], [:"$1"]} ])
# |> Enum.count()
## getting the select parameter:
## in iex:
## > Mix.install([{:ex2ms, "~> 1.0"}])
## > import Ex2ms
## > fun do {p,d,tf} = z when d <= 64 and tf == false -> p end
## (copy output)
for {l,t,d,p} <- [{:full,:cc,mod,par},{:fulli,:cc,mod,not par},
{:t1ur,:dl,t1remd,t1par}, {:t1ul,:dr,t1remd,t1par},
{:t1dl,:ur,t1remd,t1par}, {:t1dr,:ul,t1remd,t1par},
{:t2ur,:dl,t2remd,t2par}, {:t2ul,:dr,t2remd,t2par},
{:t2dl,:ur,t2remd,t2par}, {:t2dr,:ul,t2remd,t2par},
{:ax1r,:cl,ax1remd,ax1par}, {:ax2r,:cl,ax2remd,ax2par},
{:ax1l,:cr,ax1remd,ax1par}, {:ax2l,:cr,ax2remd,ax2par},
{:ax1u,:dc,ax1remd,ax1par}, {:ax2u,:dc,ax2remd,ax2par},
{:ax1d,:uc,ax1remd,ax1par}, {:ax2d,:uc,ax2remd,ax2par} ], into: %{} do
{l, :ets.select(t,[ {{:"$1", :"$2", :"$3"}, [{:andalso, {:"=<", :"$2", d}, {:==, :"$3", p}}], [:"$1"]} ]) |> Enum.count()}
end
end
def calc(grid,n) do
# precalc = prep_calc(grid,n) # 15 seconds
# |> IO.inspect()
precalc = %{ full: 7651, fulli: 7699, t1ur: 973, t1ul: 992, t1dl: 987, t1dr: 977, t2ur: 6710, t2ul: 6708, t2dl: 6715, t2dr: 6705, ax1r: 5764, ax2r: 0, ax1l: 5772, ax2l: 0, ax1u: 5767, ax2u: 0, ax1d: 5769, ax2d: 0 }
{{rc,_},_} = Enum.find(grid,fn {_,v} -> v == ?S end)
{rmax,_} = Enum.max_by(Map.keys(grid), &elem(&1,0))
mod = rmax+1
kk = div(n+1,mod)
full_tls = 1 + 4 * div(kk-1,2) * (div(kk-1,2)+1)
full_tls_i = 4 * div(kk,2) * div(kk,2)
t1diag_tls = (if rem(n+1,mod) in [0,1], do: kk-1, else: kk)
t2diag_tls = t1diag_tls - 1
ax1remd = rem(n - rc - 1,mod)
ax2_tls = (if ax1remd < rc-1, do: 1, else: 0)
full_tls * precalc[:full] + full_tls_i * precalc[:fulli] +
t1diag_tls * (precalc[:t1ur]+precalc[:t1ul]+precalc[:t1dl]+precalc[:t1dr]) +
t2diag_tls * (precalc[:t2ur]+precalc[:t2ul]+precalc[:t2dl]+precalc[:t2dr]) +
precalc[:ax1r]+precalc[:ax1l]+precalc[:ax1u]+precalc[:ax1d] +
ax2_tls * (precalc[:ax2r]+precalc[:ax2l]+precalc[:ax2u]+precalc[:ax2d])
end
def solve2(grid) do
# calc(grid,17)
calc(grid, 26501365)
end
end
:timer.tc(&Main.run/0)
|> IO.inspect(charlists: :as_lists)
1 Like
