This was way too easy after the last few days. Simple map, filter and count.
I expected a twist in part 2, but there wasn’t any. My solution:
Today’s puzzle is all about quadratic equation.
If the total time of a game is t, the speed of the boat (i.e. the time holding that button) is v, the distance the boat traveled is s, then the equation is
v * (t - v) = s
which can be normalized to
(v ** 2) - (t * v) + s = 0
All the speeds that result in better distance are between the two solutions of v of that equation.
Part 1
puzzle_input
|> String.split("\n")
|> Stream.map(&String.split/1)
|> Stream.map(&tl/1)
|> Stream.map(&Enum.map(&1, fn s -> String.to_integer(s) end))
|> Enum.zip()
|> Enum.map(fn {t, s} ->
delta = :math.sqrt(t * t - 4 * s)
v1 = ceil((t - delta) / 2)
v2 = floor((t + delta) / 2)
v2 - v1 + 1
end)
|> Enum.product()
Part 2
[t, s] =
puzzle_input
|> String.split("\n")
|> Enum.map(fn line ->
~r/\d/
|> Regex.scan(line)
|> List.flatten()
|> Enum.join()
|> String.to_integer()
end)
delta = :math.sqrt(t * t - 4 * s)
v1 = ceil((t - delta) / 2)
v2 = floor((t + delta) / 2)
v2 - v1 + 1
Aaaah. I wish I knew maths …
I hesitate to post my solution because it is so much more complex, but anyway.
Part 2 was around 4 seconds with the algorithm of part 1 so I used a binary search to find the two bounds:
defmodule AdventOfCode.Y23.Day6 do
alias AoC.Input, warn: false
def read_file(file, _part) do
file |> Input.stream!(trim: true) |> Enum.take(2)
end
def parse_input([times, distances], :part_one) do
times = int_list_no_header(times)
distances = int_list_no_header(distances)
Enum.zip(times, distances)
end
def parse_input(["Time: " <> times, "Distance: " <> distances], _) do
{single_int(times), single_int(distances)}
end
defp int_list_no_header(string) do
string
|> String.split(" ", trim: true)
|> Enum.drop(1)
|> Enum.map(&String.to_integer/1)
end
defp single_int(string) do
string
|> String.split(" ", trim: true)
|> Enum.join()
|> String.to_integer()
end
def part_one(problem) do
problem
|> Enum.map(&count_wins/1)
|> Enum.product()
end
defp count_wins({time, best}) do
0..time
|> Enum.map(&hold_time_to_distance(&1, time))
|> Enum.filter(&(&1 > best))
|> length()
end
defp hold_time_to_distance(hold = speed, time) do
duration = time - hold
_distance = speed * duration
end
def part_two({time, distance_record}) do
half = trunc(time / 2)
left = binary_search(&find_left_bound(&1, time, distance_record), 1, half)
right = binary_search(&find_right_bound(&1, time, distance_record), half, time)
right - left + 1
end
defp find_left_bound(hold, time, record) do
left = hold_time_to_distance(hold - 1, time)
right = hold_time_to_distance(hold, time)
case {left, right} do
{d1, d2} when d1 < record and d2 > record -> :eq
{_d1, d2} when d2 < record -> :lt
{d1, _d2} when d1 > record -> :gt
end
end
defp find_right_bound(hold, time, record) do
left = hold_time_to_distance(hold, time)
right = hold_time_to_distance(hold + 1, time)
case {left, right} do
{d1, d2} when d1 > record and d2 < record -> :eq
{_d1, d2} when d2 > record -> :lt
{d1, _d2} when d1 < record -> :gt
end
end
def binary_search(ask, min, max) do
n = div(min + max, 2)
case ask.(n) do
# n is lower than the answer
:lt -> binary_search(ask, n + 1, max)
# n is greater than the answer
:gt -> binary_search(ask, min, n - 1)
:eq -> n
end
end
end
And it takes less than 100µs for part 2 which is really nice.
But still, I would like to understand your maths ![]()
Your binary search part is brilliant. I know the optimal time of holding the button is just time / 2, so I could have just used your strategy.
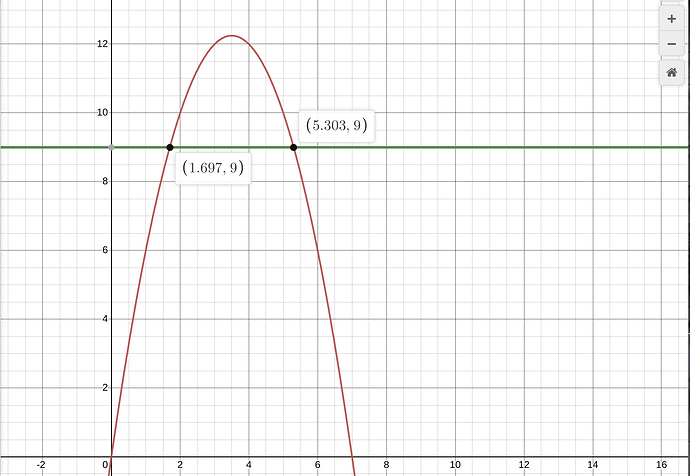
About the math in my solution, first see this image that corresponds to the first game in Part 1 (total time = 7)
The horizontal axis is the speed (i.e. time of holding the button), and the vertical axis is how far the boat can travel.
The red line shows the relationship between the speed and the distance the boat can travel.
The green line is the distance that the last winner traveled.
To beat the last winner, my speed needs to be between the two cross points (the two black points) of the red line and the green line.
The rest is just to google how to solve a quadratic equation.
Yes I figured out that the best distance would always be to hold for 0.5 * time, so I splitted my search here.
Ok so I googled a bit and that -4 seems to be inherent of this form of equation and not specific to those boats, which reassures me.
Reminds me a long time ago in high school but I guess I had already bailed out of mathematics ![]()
My beginner’s solution, Day 06.
I was considering binary search as well when coming up with an efficient solution.
But naive approach turned out to be fast enough.
defmodule Day06 do
def part2(input) do
parse(input, :part2)
|> number_of_ways_you_can_beat_the_record
end
def part1(input) do
parse(input)
|> Enum.map(&number_of_ways_you_can_beat_the_record/1)
|> Enum.product
end
def number_of_ways_you_can_beat_the_record({time, record}) do
for n <- 1..time-1 do (time - n) * n end
# |> Enum.count(fn x -> x > record end)
|> Enum.count(&Kernel.>(&1,record))
end
def parse(raw_document, :part2) do
raw_document
|> String.replace(" ", "")
|> parse
|> List.first
# {71530, 940200}
end
def parse(raw_document) do
# "Time: 7 15 30
# Distance: 9 40 200"
raw_document
|> String.split("\n")
|> Enum.map(fn raw_line -> raw_line
|> String.split(":")
|> List.last
|> String.split
|> Enum.map(&String.to_integer/1)
end)
|> List.zip
# [{7, 9}, {15, 40}, {30, 200}]
end
end
Inspired by the solution of @lud , I just tried another approach with Newton’s approximation because I don’t want to deal with floating point numbers ![]()
Prep
# Newton's approximation of one of the solutions to the equation
#
# (v ** 2) - (t * v) + s = 0
#
# Keep only the integer part.
approx = fn t, s, v ->
v
|> Stream.unfold(fn v ->
y = v * v - t * v + s
k = 2 * v - t
dv = div(y, k)
{v, v - dv}
end)
|> Stream.chunk_every(2, 1)
|> Enum.find(&match?([a, a], &1))
|> hd()
end
Part 2
t = ... # The total time
s = ... # The distance the last champion traveled
approx.(t, s, t) - approx.(t, s, 0) - 1
I also considered the last race (when function breaking points are integers), that why my floor and ceil methods are more complicated:
defmodule AdventOfCode.Day06 do
def part1(input) do
calculate(input, fn numbers -> Enum.map(numbers, &String.to_integer/1) end)
end
def part2(input) do
calculate(input, fn numbers -> [Enum.join(numbers) |> String.to_integer()] end)
end
defp calculate(input, mapping_function) do
input
|> String.split("\n", trim: true)
|> Enum.map(fn line ->
[_ | numbers] = String.split(line, ~r/\s+/)
mapping_function.(numbers)
end)
|> Enum.zip()
|> Enum.map(&count_wins/1)
|> Enum.product()
end
defp count_wins({time, distance}) do
delta = :math.sqrt(time * time - 4 * distance)
x1 = (time + delta) / 2
x2 = (time - delta) / 2
to_floor(x1) - to_ceil(x2) + 1
end
defp to_ceil(x) do
truncated = trunc(x)
if truncated == x, do: truncated + 1, else: ceil(x)
end
defp to_floor(x) do
truncated = trunc(x)
if truncated == x, do: truncated - 1, else: floor(x)
end
end
I thought of that, too, but fortunately, my input doesn’t have that problem ![]()
Anyway, the Newton’s approximation approach should be fine in all cases.
I was happy to see a problem today that didn’t take me hours to solve.
While I knew there was an equation to solve it in an instant, I didn’t bother to look it up and just iterated over the whole problem space.
I fully expected an order of magnitude that required the mathematical approach in part 2, but was surprised that my trivial approach just took 4 seconds to run on part 2.
(Using Erlang for the fun right now:)
a(In) ->
[T, D] = [parse(L) || L <- In],
G = [opt(Time, Dist) || {Time, Dist} <- lists:zip(T, D)],
lists:foldl(fun(X, Acc) -> X * Acc end, 1, G).
parse(L) -> [list_to_integer(I) || I <- tl(re:split(L, "\\s+", [trim, {return, list}]))].
opt(Time, Dist) -> length([1 || R <- lists:seq(1, Time), R * (Time - R) > Dist]).
b(In) ->
[T, D] = [list_to_integer(parse_join(L)) || L <- In],
opt(T, D).
parse_join(L) -> lists:concat([I || I <- tl(re:split(L, "\\s+", [trim, {return, list}]))]).
There might even be an off by 1 error in my code (> Dist or >= Dist?), but it still worked on both example an my input.
Probably I’ll clean it up and try to implement the efficient solution in the evening, thanks for the great explanation @Aetherus
I did write out the quadratic equation for this one! But I couldn’t remember how to solve it, so I just brute forced the solution. It took 70 seconds.
It is always fun to see code changes between parts. But this time only input file had to be changed ![]()
I used quadratic equation and just in case assumed error of up to 1.0.
I was wondering why this is so slow in Elixir compared to Erlang. I thought your solution should be faster because you used Streams so it doesn’t have to initialize the List upfront. However, in Elixir Livebook it took >100s to complete, while my primitive Erlang solution was done in <4s.
Then I tried it in the Eshell and it was as slow as Elixir.
Livebook: 73s
IEx: 50s
elixir bench.ex: 3.2s
for the exact same code:
for r <- 1..46828479, r * (46828479 - r) > 347152214061471 do 1 end |> Enum.count() |> IO.puts
Does anyone have an idea why Livebook and IEx is so much slower? Is it possible it’s not doing any JIT, or am I doing something wrong?
Erlang/OTP 25 [erts-13.2] [source] [64-bit] [smp:16:16] [ds:16:16:10] [async-threads:1] [jit:ns]
Elixir 1.15.7 (compiled with Erlang/OTP 25)
Livebook 0.11.4
This is due to compiled versus interpreted code.
In this case, wrapping this within a module inside livebook/IEx will compile the code and run in ~1s, while just running the code directly in interpreted mode (uses :erl_eval under the hood) will be slow when you have many iterations.
defmodule MyCell do
def run do
for r <- 1..46828479, r * (46828479 - r) > 347152214061471 do 1 end |> Enum.count()
end
end
MyCell.run()
I realised we could avoid computing the whole range and get away with only half of it, as the times once you go over time/2 repeat:
def count_winning(race, record) do
scores = for n <- 1..div(race, 2), do: n * (race - n)
[_middle | rev_no_middle] = reversed = Enum.reverse(scores)
scores = scores ++ if rem(race, 2) == 1, do: reversed, else: rev_no_middle
Enum.count(scores, fn score -> score > record end)
end
However I didn’t notice we could use the quadratic equation, or solve it with binary search. Good job I checked the forum otherwise I’d be feeling pretty clever. Thanks for sharing ![]()
edit: whoops, I even forgot to implement the part that only counts half the list ![]()
Simple one today
defp ways_to_win(race) do
Enum.count(1..race.time, fn held_seconds ->
traveled = held_seconds * (race.time - held_seconds)
traveled > race.distance
end)
end
Full solution here on Github
I used the quadratic formula, so part 2 was a non-issue.
The trickiest part of this was a corner-case for some inputs where the racer can end up getting exactly the same distance as the record, which shouldn’t count. I solved this by adding a tiny additional distance, breaking the numerical coincidence.
defmodule Day6Part1 do
@regex ~r{Time:\s+([\d\s]+\d)\s+Distance:\s+([\d\s]+\d)}
def read(filename) do
data = File.read!(filename)
[time_str, distance_str] = Regex.run(@regex, data, capture: :all_but_first)
Enum.zip(parse(time_str), parse(distance_str))
end
defp parse(s) do
s
|> String.split(~r{\s+})
|> Enum.map(&String.to_integer/1)
end
def endpoints({t, d}) do
base = t/2
half_width = :math.sqrt(t*t/4 - (d+0.001))
{ceil(base - half_width), floor(base + half_width)}
end
end
Day6Part1.read("input.txt")
|> Enum.map(&Day6Part1.endpoints/1)
|> Enum.map(fn {a, b} -> b - a + 1 end)
|> Enum.product()
|> IO.inspect()
I’m very late for the party. But here’s my solution.
I didn’t know about the quadratic equation, that’s very cool.
My approach was this: there’s a pattern where after you get the number of holding times that failed to beat the best distance until the first time that beats it, you can use that number to calculate the holding times to beat the distance by multiplying it by 2 and then subtract it by the race_time + 1 (the + 1 is to include the scenario for the 0 holding time)
The main piece is this:
def count_holding_time_to_beat_record(race_time, distance_to_beat) do
0..race_time
|> Enum.reduce_while(0, fn holding_time, acc ->
distance_reached = calculate_distance(holding_time, race_time)
if distance_reached > distance_to_beat do
number_of_fails_for_race = acc * 2
{:halt, race_time + 1 - number_of_fails_for_race}
else
{:cont, acc + 1}
end
end)
end